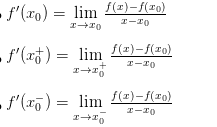Hiểu được những khó khăn của học sinh khi mới bắt đầu học tính đạo hàm, WElearn đã tổng hợp lại tất các các công thức đạo hàm thường gặp, các quy tắc của đạo hàm, cách tính đạo hàm bằng máy tính và đặc biệt là các dạng bài tập về đạo hàm thường gặp. Các bạn cùng theo dõi nhé!
Định nghĩa đạo hàm là gì?
Cho hàm số y = f(x) xác định trên khoảng (a;b), x0 ∈ (a;b). Khi x → x0, giới hạn hữu hạn (nếu có) của tỉ số là đạo hàm của hàm số đã cho tại x0.
Kí hiệu là f'( x0) hay y'( x0). Như vậy: f'( x0 ) =
Nếu đặt x – x0 = ∆x và ∆y = f(x0+∆x) – f(x0) thì ta có
f'(x0) =
Đại lượng ∆x được gọi là số gia của đối số tại x0 và đại lượng ∆y được gọi là số gia tương ứng của hàm số.
Quy tắc cơ bản của đạo hàm
Tổng hợp các công thức đạo hàm lớp 11 (đầy đủ)
Công thức đạo hàm cơ bản
Công thức đạo hàm của hàm hợp
Cho hàm số y = f(u) với u = u(x) thì ta có: y′u=y′u.u′x
Công thức đạo hàm cấp cao
Công thức đạo hàm lượng giác
Công thức đạo hàm logarit
Công thức đạo hàm số mũ
Công thức đạo hàm của một số phân thức hữu tỉ
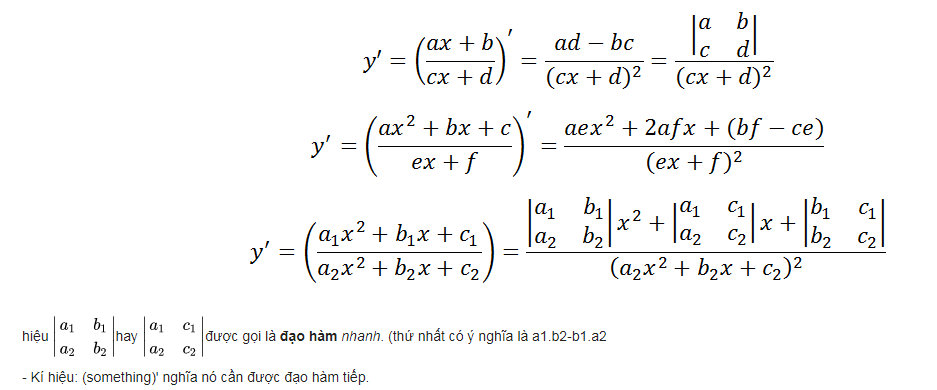
Cách tính đạo hàm bằng máy tính
Để thực hiện tính đạo hàm bằng máy tính, bạn thực hiện các bước sau:

Các dạng bài toán liên quan đến công thức đạo hàm
Dạng 1. Tính đạo hàm bằng định nghĩa
Hàm số y = f(x) có đạo hàm tại điểm x= x0 <=> f'(x0+)=f'(x0–)
Hàm số y = f(x) có đạo hàm tại điểm thì trước hết phải liên tục tại điểm đó.
Ví dụ 1: f(x) = 2x3+1 tại x=2
=> f'(2) = 24
Dạng 2: Chứng minh các đẳng thức về đạo hàm
Ví dụ 1: Cho y = e−x.sinx, chứng minh hệ thức y”+2y′+ 2y = 0
Bài giải :
Ta có y′=−e−x.sinx + e−x.cosx
y′ =−e−x.sinx+e−x.cosx
y”=e−x.sinx−e−x.cosx−e−x.cosx−e−x.sinx = −2e−x.cosx
Vậy y”+ 2y′+ 2y = −2.e−x.cosx− −2.e−x.sinx + 2.e−x.cosx + 2.e−x.sinx =0
Dạng 3: Viết phương trình tiếp tuyến khi biết tiếp điểm
Phương trình tiếp tuyến của đường cong (C): y= f(x) tại tiếp điểm M( x0;y0) có dạng:
Ví dụ: Cho hàm số y= x3+3mx2 + ( m+1)x + 1 (1), m là tham số thực. Tìm các giá trị của m để tiếp tuyến của đồ thị của hàm số (1) tại điểm có hoành độ x = -1 đi qua điểm A( 1;2).
Tập xác định D = R
y’ = f'(x)= 3x2 + 6mx + m + 1
Với x0 = -1 => y0 = 2m -1, f'( -1) = -5m + 4
Phương trình tiếp tuyến tại điểm M( -1; 2m – 1) : y= ( -5m + 4 ) ( x+1) + 2m -1 (d)
Ta có A ( 1;2) ∈ (d) <=> ( -5m + 4).2 + 2m – 1 = 2 => m = 5/8
Dạng 4: Viết phương trình tiếp khi biết hệ số góc
Viết PTTT Δ của ( C ) : y = f( x ), biết Δ có hệ số góc k cho trước
Gọi M( x0;y0) là tiếp điểm. Tính y’ => y'(x0)
Do phương trình tiếp tuyến Δ có hệ số góc k => y’ = ( x0) = k (i)
Giải (i) tìm được x0 => y0= f(x0) => Δ : y = k (x – x0)+ y0
Lưu ý:Hệ số góc k = y'( x0) của tiếp tuyến Δ thường cho gián tiếp như sau:
Ví dụ: Cho hàm số y=x3+3x2-9x+5 ( C). Trong tất cả các tiếp tuyến của đồ thị ( C ), hãy tìm tiếp tuyến có hệ số góc nhỏ nhất.
Ta có y’ = f'( x ) = 3x2 + 6x – 9
Gọi x0 là hoành độ tiếp điểm của tiếp tuyến, vậy f'( x0) = 3 x02 + 6 x0 – 9
Ta có 3 x02 + 6 x0 – 9 =3 ( x02 + 2x0 +1) – 12 = 3 (x0+1)2– 12 > – 12
Vậy min f( x0)= – 12 tại x0 = -1 => y0=16
Suy ra phương trình tiếp tuyến cần tìm: y= -12( x+1)+16 <=> y= -12x + 4
Dạng 5: Phương trình và bất phương trình có đạo hàm
Như vậy, bài viết đã tổng hợp lại tất cả những Công thức đạo hàm chi tiết và đầy đủ nhất để giúp bạn giải quyết các bài tập liên quan đến đạo hàm trong nháy mắt. Hy vọng những kiến thức mà chúng mình chia sẻ có ích cho việc học của bạn. Chúc bạn thành công nhé!
TRUNG TÂM GIA SƯ WELEARN
- Địa chỉ 1: 38 Đ. Số 23, Linh Chiểu, Thủ Đức, Thành phố Hồ Chí Minh.
- Địa chỉ 2: 104 Hồ Văn Tư, Trường Thọ, Thủ Đức, Thành phố Hồ Chí Minh.
- Hotline: 0906782291
- Mail: welearnvietnam@gmail.com
- Website: https://welearnvn.com/
- Fanpage: WELearn Gia Sư